第三章
主要内容
- 确定有限自动机
- 非确定有限自动机
- 确定与非确定有限自动机的等价性
- 右线性文法和有限自动机的等价性
- 右线性文法的性质(泵浦定理)
- 只用归纳法进行证明的方法
第一节 有限自动机
有限自动机的概念
具有离散输入输出系统的一种数学模型(可以没有输出,比较特殊的也可以没有输入)
有限的状态
状态+输入--->状态转移
每次转换的后继状态都唯一 ---> DFA
每次转换的后继状态不唯一 ---> NFA
DFA Deterministic finite automaton
NFA Non Deterministic finite automaton
DFA的形式定义
定义:DFA是一个五元组M=(Q,T,δ,q0,F)
- Q: 有限的状态集合
- T: 有限的输入字母表
- δ: 转换函数(状态转移集合): Q×T ---> Q
- q0: 初始状态, q0 ∈ Q
- F: 终止状态集, F ∈ Q
转移图表示的DFA

转移表表示的DFA
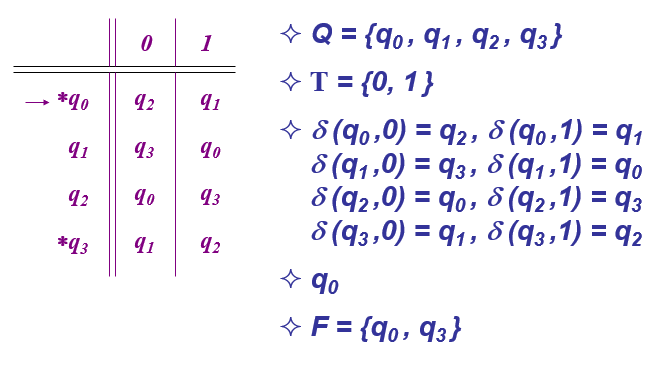
扩展转移函数适合于输入字符串
δ’函数:接收一个字符串的状态转移函数。 δ’ : Q x T* ---> Q
对任何q ∈ Q,定义:
1.δ’ (q , e ) = q
2.若ω是一个字符串, a是一个字符,定义: δ’(q,ωa)=δ(δ’(q,ω),a)
对于DFA,δ’(q,a)=δ(δ‘(q, e ),a)=δ(q,a),即对于单个字符时δ和δ'是相等的。为了方便,以后在不引起混淆时用δ代替δ'
被DFA接受的语言
n被DFA接收的字符串: 输入结束后使DFA的状态到达终止状态。否则,该字符串不能被DFA接收.
DFA接收的语言: 被DFA接收的字符串的集合.
L(M) = { ω | δ’ ( q0 , ω) ∈ F }
格局
为描述有限自动机的工作过程,对于它在某一时刻的工作状态,可用两个信息表明:当前状态q,待输入字符串ω。两者构成一个瞬时描述,用(q, ω)表示,称为格局。
初始格局:(q0, ω)
终止格局: (q, ε), q∈F
有限状态机是无记忆的,接受不同的字符串可以进入同一格局
设计有限自动机
自动机的设计是一个创造过程,没有简单的算法或过程。
技巧:假设自己是机器,思考如何去实现机器的任务。
为判断到目前为止所看到的字符串是否满足某个语言,须估算出读一个字符串时需要记住哪些关键的东西。
例1:构造自动机,识别所有由奇数个a和奇数个b组成字符串。
关键:不需要记住所看到的整个字符串,只需记住至此所看到的a、b个数是偶数还是奇数。

第二节 不确定的有限自动机(NFA)
修改DFA的模型,使之在某个状态, 对应一个输入,可以有多个转移, 到达不同的状态, 即:具有同时处于几个状态的能力。则称为不确定的有限自动机。
不确定有限自动机的形式定义
nNFA是一个五元组,M=(Q,T,δ,q0,F).
其中δ是Q×T->2^Q的函数, 其余与DFA相同.
n如果接收一个字符串后NFA进入一个状态集,而此集合中包含一个或以上F中的状态, 则称NFA接收该字符串.
数学上如何表达多个状态呢?使用幂集状态子集。
设X是一个非空集合,由X的一切子集(包括空集,X自身)为元素形成的集合称为X的幂集。有n个元素形成的集合的幂集共有2的n次方个元素。
转移图和转移表表示的NFA


格局示例

n如图所示,用格局序列描述自动机的工作过程,当输入字符串是011011时,则有

NFA的状态扩展函数
δ可扩展为δ’ (δ’ : Q x T* ---> 2^Q)
1.δ'(q, ε) = {q} 含义: 不允许无输入的状态变化.
2.δ'(q,ωa)={p|存在r∈δ'(q,ω)∧p∈δ(r,a)}
含义:δ‘(q,ωa)对应的状态集合是δ’(q,ω)对应的每个状态下再接收字符a以后可能到达的状态集合的并集.
NFA接受的语言
设一个 NFA A = (Q, T, d, q0 , F )
定义 A 的语言:
L(A) = { ω | δ' ( q0 , ω) ∩ F != ∅ }
第三节 NFA与DFA的等价性
DFA是NFA的特例(DFA本身就是NFA), 所以NFA必然能接收DFA能接收的语言. 因此证明等价性只要能够证明一个NFA所能接收的语言必能被另一个DFA所接收。
定理: 设一个NFA接受语言L, 那么必然存在一个DFA接受L。
证明:
策略:对于任意一个NFA,构造一个接收它所能接收语言的DFA,这个DFA的状态对应了NFA的状态集合。

步骤:
- 初始的NFA

- 子集构造,计算状态可达

- 经筛选后的DFA

证明:从NFA构造等价的DFA




Comments NOTHING