【北邮大三上操作系统】第五组多核多线程编程及性能分析

目录显示

第五组多核多线程编程及性能分析

1 实验要求

参照参考文献“利用多核多线程进行程序优化”，在 Linux 环境下，编写多线程程序，分析以下几个因素对程序运行时间的影响：

程序并行化
线程数目
共享资源加锁
CPU 亲和
cache 优化

掌握多 CPU、多核硬件环境下基本的多线程并行编程技术。

实验内容包括：

实验 5.1 观察实验平台物理 cpu、cpu 核和逻辑 cpu 的数目
实验 5.2. 单线程/进程串行 vs 两线程并行 vs 三线程加锁并行程序对比
实验 5.3. 三线程加锁 vs 三线程不加锁对比
实验 5.4. 针对 Cache 的优化
实验 5.5. CPU 亲和力对并行程序影响
八种实现方案运行时间对比总结

2 实验环境

硬件：Intel(R) Xeon(R) Platinum 8163 CPU，主频3.5GHz，内存30G

软件：CentOS Linux release 7.9.2009，内核版本Linux-3.10.0

3 实验内容1 观察实验平台物理 cpu、CPU 核和逻辑 cpu 的数目

3.1 实验目的

观察实验所采用的计算机（微机、笔记本电脑）物理 cpu、CPU 核和逻辑 cpu 的数目

物理 cpu 数目：主板上实际插入的 cpu 数量，可以数不重复的 physical id 有几个（physical id）。

多路服务器、大型主机系统、集群系统一般可以配置多个物理 CPU；常规微机、笔记本电脑一般只配备 1 个物理 CPU；
cpu 核（cpu cores）的数目：单块 CPU 上面能处理数据的芯片组的数量，如双核、四核等；
逻辑 cpu 数目：

对不支持超线程 HT 的 CPU，逻辑 cpu 数目=物理 CPU 个数×每颗 CPU 核数，

对支持超线程 HT 的 CPU，逻辑 cpu 数目=物理 CPU 个数×每颗 CPU 核数*2

3.2 实验方法

通过下列命令查看 cpu 相关信息

物理cpu数：

grep 'physical id' /proc/cpuinfo|sort|uniq|wc -l

cpu 核数：

grep 'cpu cores' /proc/cpuinfo|uniq|awk -F ':' '{print $2}'

逻辑 cpu：

cat /proc/cpuinfo| grep "processor"|wc -l

3.3 运行结果及分析

可以看出我的服务器，单cpu，2核，有超线程。

执行命令lscpu也可以看到相关信息：

4 实验内容2 单线程/进程串行 vs 2 线程并行 vs 3 线程加锁并行程序

4.1 实验目的

参照参考文献“利用多核多线程进行程序优化”，在 Linux 环境下，编写多线程程序，分析以下几个因素对程序运行时间的影响：

程序并行化
线程数目
共享资源加锁
CPU 亲和
cache 优化

掌握多 CPU、多核硬件环境下基本的多线程并行编程技术。

4.2 实验内容

实验 5.1 观察实验平台物理 cpu、cpu 核和逻辑 cpu 的数目
实验 5.2. 单线程/进程串行 vs 两线程并行 vs 三线程加锁并行程序对比
实验 5.3. 三线程加锁 vs 三线程不加锁对比
实验 5.4. 针对 Cache 的优化
实验 5.5. CPU 亲和力对并行程序影响
八种实现方案运行时间对比总结

4.3 实验设计原理

医生治病首先要望闻问切，然后才确定病因，最后再对症下药，如果胡乱医治一通，不死也残废。说起来大家都懂的道理，但在软件优化过程中，往往都喜欢犯这样的错误。不分青红皂白，一上来这里改改，那里改改，其结果往往不如人意。

一般将软件优化可分为三个层次：系统层面，应用层面及微架构层面。首先从宏观进行考虑，进行望闻问切，即系统层面的优化，把所有与程序相关的信息收集上来，确定病因。确定病因后，开始从微观上进行优化，即进行应用层面和微架构方面的优化。

系统层面的优化：内存不够，CPU 速度过慢，系统中进程过多等
应用层面的优化：算法优化、并行设计等
微架构层面的优化：分支预测、数据结构优化、指令优化等

软件优化可以在应用开发的任一阶段进行，当然越早越好，这样以后的麻烦就会少很多。

利用并行程序设计模型来设计应用程序，就必须把自己的思维从线性模型中拉出来，重新审视整个处理流程，从头到尾梳理一遍，将能够并行执行的部分识别出来。

可以将应用程序看成是众多相互依赖的任务的集合。将应用程序划分成多个独立的任务，并确定这些任务之间的相互依赖关系，这个过程被称为分解（Decomosition）。分解问题的方式主要有三种：任务分解、数据分解和数据流分解。

在实际应用程序中，采用最多的是应用层面的优化，也会采用微架构层面的优化。将某些优化和维护成本进行对比，往往选择的都是后者。如分支预测优化和指令优化，在大型应用程序中，往往采用的比较少，因为维护成本过高。

本文将从应用层面和微架构层面，对样例程序进行优化。

对于应用层面的优化，将采用多线程和 CPU 亲和力技术；
在微架构层面，采用 Cache 优化。

最后，总结对比单线程/进程串行程序和其它 7 种多线程并行程序的运行时间，并以图表方式给出具体结果。

要求：

以柱状图形式表示上述 5 种情况下程序运行时间的定量测试结果（运行时间）
分析对比程序并行化、线程数目、共享资源加、CPU 亲和、cache 优化对程序运行时间的影响，结合程序/进程自身业务逻辑、相互间同步互斥关系等分析解释运行时间产生差异的原因

4.4 实验步骤

步骤一单线程/样例程序

首先，定义如下数据结构：

#define ORANGE_MAX_VALUE 1000000
#define APPLE_MAX_VALUE 100000000

struct apple {
  unsigned long long a;
  unsigned long long b;
};

struct orange {
  int a[ORANGE_MAX_VALUE];
  int b[ORANGE_MAX_VALUE];
};

程序功能为：

求从1一直到 APPLE_MAX_VALUE (100000000) 相加累计的和，并赋值给 apple 的 a 和 b ；求 orange 数据结构中的 a[i]+b[i] 的和，循环ORANGE_MAX_VALUE(1000000) 次。

步骤二 2线程

仔细分析样例程序，运用任务分解的方法，不难发现计算 apple 的值和计算 orange 的值，属于完全不相关的两个操作，因此可以并行，改造为两线程程序。

步骤三 3线程加锁

更甚一步，通过数据分解的方法，还可以发现，计算 apple 的值可以分解为两个线程，一个用于计算 apple a 的值，另外一个线程用于计算 apple b 的值 (说明：本方案抽象于实际的应用程序)。但两个线程存在同时访问 apple 的可能性，所以需要加锁访问该数据结构。因此，程序可以改造为3线程加锁程序。

步骤四 3线程不加锁

针对加锁的三线程方案，由于两个线程访问的是 apple 的不同元素，根本没有加锁的必要，所以修改 apple 的数据结构（删除读写锁代码），通过不加锁来提高性能，将程序改造为3线程不加锁的程序。

步骤五 cache优化3线程不加锁

不加锁三线程方案的瓶颈在于 cache，那么让 apple 的两个成员 a 和 b 位于不同的 cache 行中，使用cache优化3线程不加锁的方案，查看效率是否有提高。

步骤六 cache优化3线程加锁

如果对加锁三线程方案中的 apple 数据结构也增加一行类似功能的代码，使用cache优化3线程加锁的方案，效率也是否会提升呢？性能不会有所提升，其原因是加锁的三线程方案效率低下的原因不是 Cache 失效造成的，而是那把锁。

步骤七 2线程设置cpu硬亲和力

CPU 硬亲和力是指进程固定在某个处理器上运行，而不是在不同的处理器之间进行频繁的迁移。这样不仅改善了程序的性能，还提高了程序的可靠性。在双核机器上，针对两线程的方案，如果将计算 apple 的线程绑定到一个 CPU 上，将计算 orange 的线程绑定到另外一个 CPU 上，效率是否会有所提高呢？观察2线程设置cpu硬亲和力的方案。

步骤八 3线程设置cpu硬亲和力

样例程序大部分时间都消耗在计算 apple 上，如果将计算 a 和 b 的值，分布到不同的 CPU 上进行计算，同时考虑 Cache 的影响，效率是否也会有所提升呢？观察3线程设置cpu硬亲和力的方案。

步骤九使用k-best方法计算每种方案的执行时间并统计

假设重复的执行一个程序，并纪录 K 次最快的时间，如果发现测量的误差 ε 很小，那么用测量的最快值表示过程的真正执行时间，称这种方法为“ K 次最优（K-Best）方法”，要求设置三个参数：

K: 要求在某个接近最快值范围内的测量值数量。

ε 测量值必须多大程度的接近，即测量值按照升序标号 V1, V2, V3, … , Vi, … ，同时必须满足（1+ ε）Vi >= Vk

M: 在结束测试之前，测量值的最大数量。

这种方法是说，对于测试数据而言，可选择测量时间值最快的K个数据，这K个数据需满足误差不超过给定上限e，并且给定一个测量数据的上限M。测量方法的收敛定义为：已经选出K个数据并满足误差e，且测量总数未超过M。如果 M 次后，不能满足误差标准，则称为不能收敛。

在接下来的所有试验中，采用 K=10，ε=2%，M=200 来获取程序运行时间，同时也对 K 次最优测量方法进行了改进，不是采用最小值来表示程序执行的时间，而是采用 K 次测量值的平均值来表示程序的真正运行时间。

4.5 实验结果及分析

首先使用以下命令编译程序：

gcc core.c -o core -lpthread

注：为了便于阅读，以下实验结果均使用文字粘贴的形式。完整实验结果以及截图请查看附件。

方案一单线程/样例程序运行结果

运行命令./core 1，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 1
0: 247079 us
1: 251961 us
2: 242715 us
3: 246068 us
4: 244605 us
5: 244865 us
6: 246890 us
7: 249237 us
8: 245200 us
9: 252912 us
10: 248470 us
11: 246115 us
12: 245750 us
13: 252464 us
14: 249290 us
15: 244586 us
break when i = 15
242715
244586
244605
244865
245200
245750
246068
246115
246890
247079
ave = 245387

该结果的含义为，在运行到i = 15的次数时，按照误差e = 2%的要求，结果已经收敛。此时输出最短时间的十次，与这十次的平均时间(um)。

方案二 2线程运行结果

运行命令./core 2，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 2
0: 330504 us
1: 329925 us
2: 329197 us
3: 331537 us
4: 331201 us
5: 331827 us
6: 331890 us
7: 330583 us
8: 331868 us
9: 331370 us
break when i = 9
329197
329925
330504
330583
331201
331370
331537
331827
331868
331890
ave = 330990

方案三 3线程加锁运行结果

运行命令./core 3，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 3
0: 584167 us
1: 576717 us
2: 578642 us
3: 581102 us
4: 577009 us
5: 576732 us
6: 577949 us
7: 579110 us
8: 578838 us
9: 582147 us
break when i = 9
576717
576732
577009
577949
578642
578838
579110
581102
582147
584167
ave = 579241

方案四 3线程不加锁运行结果

运行命令./core 3，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 4
0: 669841 us
1: 661561 us
2: 680345 us
3: 650117 us
4: 643086 us
5: 645143 us
6: 1225782 us
7: 1050413 us
8: 985881 us
9: 868815 us
10: 1244577 us
11: 1231272 us
12: 1229973 us
13: 630369 us
14: 1282727 us
15: 1275831 us
16: 1224734 us
17: 1235469 us
18: 639672 us
19: 646181 us
20: 653500 us
21: 1026539 us
22: 1309693 us
23: 1201069 us
24: 1178396 us
25: 646340 us
26: 1287034 us
27: 699103 us
28: 786617 us
29: 722786 us
30: 621392 us
31: 655178 us
32: 589689 us
33: 626177 us
34: 637984 us
35: 631458 us
36: 638873 us
37: 1266524 us
38: 1281039 us
39: 1275692 us
40: 1319328 us
41: 1320941 us
42: 673564 us
43: 1270562 us
44: 1082509 us
45: 624231 us
46: 631817 us
47: 651681 us
48: 1205875 us
49: 1207337 us
50: 1024041 us
51: 1178656 us
52: 1135735 us
53: 668482 us
54: 669178 us
55: 1158942 us
56: 654793 us
57: 653304 us
58: 1148715 us
59: 1130186 us
60: 1213313 us
61: 1233556 us
62: 1116415 us
63: 653683 us
64: 629235 us
65: 625234 us
66: 1112471 us
67: 666282 us
68: 676149 us
69: 724026 us
70: 957132 us
71: 664699 us
72: 1170905 us
73: 1208428 us
74: 1236392 us
75: 1214011 us
76: 1241794 us
77: 639737 us
78: 625502 us
79: 1142231 us
80: 1074249 us
81: 1209275 us
82: 1192816 us
83: 1159676 us
84: 1197565 us
85: 641503 us
86: 1248510 us
87: 1176431 us
88: 915673 us
89: 637940 us
90: 1232331 us
91: 1210449 us
92: 1153815 us
93: 636252 us
94: 1266479 us
95: 870960 us
96: 1245260 us
97: 693877 us
98: 669818 us
99: 666391 us
100: 681687 us
101: 1281317 us
102: 1282064 us
103: 1266929 us
104: 893189 us
105: 615314 us
106: 1214084 us
107: 656264 us
108: 631186 us
109: 631721 us
110: 1233366 us
111: 1234887 us
112: 1225858 us
113: 1227546 us
114: 1303756 us
115: 1257103 us
116: 684435 us
117: 686757 us
118: 653773 us
119: 694059 us
120: 655205 us
121: 791860 us
122: 616708 us
123: 675172 us
124: 1086611 us
125: 1193082 us
126: 1188875 us
127: 1315580 us
128: 1279353 us
129: 1169398 us
130: 642543 us
131: 629593 us
132: 624152 us
133: 639702 us
134: 625417 us
135: 626926 us
136: 1087482 us
137: 789271 us
138: 1162537 us
139: 1127592 us
140: 1176000 us
141: 1261535 us
142: 827132 us
143: 1088817 us
144: 1263486 us
145: 1216488 us
146: 1247795 us
147: 691489 us
148: 633648 us
149: 1240512 us
150: 1210885 us
151: 1165709 us
152: 1237301 us
153: 964392 us
154: 623031 us
155: 1195233 us
156: 685824 us
157: 1225670 us
158: 986932 us
159: 605027 us
160: 609472 us
161: 646258 us
162: 608477 us
163: 629688 us
164: 741802 us
165: 1219227 us
166: 646038 us
167: 649299 us
168: 650314 us
169: 644190 us
170: 1178048 us
171: 734806 us
172: 1226330 us
173: 677354 us
174: 616153 us
175: 1075455 us
176: 630885 us
177: 662670 us
178: 672546 us
179: 665495 us
180: 677727 us
181: 674083 us
182: 672168 us
183: 678293 us
184: 769666 us
185: 775147 us
186: 608388 us
187: 723804 us
188: 636905 us
189: 608653 us
190: 712307 us
191: 643355 us
192: 1282720 us
193: 1268194 us
194: 644625 us
195: 628791 us
196: 629463 us
197: 666222 us
198: 632263 us
199: 638246 us
Done!
589689
605027
608388
608477
608653
609472
615314
616153
616708
621392
ave = 609927

可以看出，在3线程不加锁的方案非常不稳定，测量时间有时相差两倍。使用k-best测量方法，实验达到200次后，最快十次的误差也没有小于2%，该方案不收敛。最后统计使用最快十次的测量结果，但实际上由于该方案的不稳定，每一次的运行结果都有差异。

方案五 cache优化3线程不加锁运行结果

首先，运行命令./core 51，验证设置cache = 32的情况。

运行结果一：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 51
0: 290052 us
1: 290421 us
2: 290265 us
3: 288412 us
4: 290176 us
5: 289710 us
6: 289928 us
7: 289610 us
8: 292888 us
9: 291353 us
break when i = 9
288412
289610
289710
289928
290052
290176
290265
290421
291353
292888
ave = 290281

运行结果二：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 51
0: 686163 us
1: 1260278 us
2: 1220356 us
3: 900088 us
4: 771120 us
5: 644669 us
6: 1006439 us
7: 701787 us
8: 1018133 us
9: 1103947 us
10: 705373 us
11: 641914 us
12: 636652 us
13: 652450 us
14: 704889 us
15: 709462 us
16: 697347 us
17: 687845 us
18: 685733 us
19: 691915 us
20: 708688 us
21: 654586 us
22: 1062518 us
23: 829309 us
24: 581543 us
25: 1056024 us
26: 1092542 us
27: 620537 us
28: 665656 us
29: 659054 us
30: 1123204 us
/*由于结果过程手动省略了部分结果*/
190: 1053045 us
191: 1175651 us
192: 682393 us
193: 664193 us
194: 665383 us
195: 662883 us
196: 669583 us
197: 741275 us
198: 1187675 us
199: 1220206 us
Done!
537098
548066
552782
552790
563695
568153
571391
576706
577719
581543
ave = 562994

多次运行改程序，发现运行结果相差甚远。有时可以快速收敛；有时则时分不稳定，不能收敛。将在后文中分析原因。

其次，运行命令./core 52，验证设置cache = 64的情况，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 52
0: 290694 us
1: 289706 us
2: 291507 us
3: 292389 us
4: 292741 us
5: 291248 us
6: 291763 us
7: 291429 us
8: 292275 us
9: 292499 us
break when i = 9
289706
290694
291248
291429
291507
291763
292275
292389
292499
292741
ave = 291625

最后，运行命令./core 53，验证设置cache = 128的情况，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 53
0: 291675 us
1: 292284 us
2: 292018 us
3: 291331 us
4: 292066 us
5: 292317 us
6: 292437 us
7: 292156 us
8: 291722 us
9: 292431 us
break when i = 9
291331
291675
291722
292018
292066
292156
292284
292317
292431
292437
ave = 292043

方案六 cache优化3线程加锁运行结果

运行命令./core 6，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 6
0: 580039 us
1: 583007 us
2: 583409 us
3: 584047 us
4: 583779 us
5: 581629 us
6: 580125 us
7: 579715 us
8: 579770 us
9: 574687 us
break when i = 9
574687
579715
579770
580039
580125
581629
583007
583409
583779
584047
ave = 581020

方案七 2线程设置cpu硬亲和力运行结果

运行命令./core 7，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 7
0: 326898 us
1: 330095 us
2: 329717 us
3: 329027 us
4: 329315 us
5: 330513 us
6: 329084 us
7: 329384 us
8: 329624 us
9: 327609 us
break when i = 9
326898
327609
329027
329084
329315
329384
329624
329717
330095
330513
ave = 329126

方案八 3线程设置cpu硬亲和力运行结果

运行命令./core 8，结果如下：

[root@iZuf67lmfh9fmh4kt2tj1tZ ~]# ./core 8
0: 291216 us
1: 294163 us
2: 294740 us
3: 294756 us
4: 292137 us
5: 292881 us
6: 291323 us
7: 358787 us
8: 359635 us
9: 358513 us
10: 358705 us
11: 293633 us
12: 292052 us
13: 293695 us
break when i = 13
291216
291323
292052
292137
292881
293633
293695
294163
294740
294756
ave = 293059

实验结果统计与分析

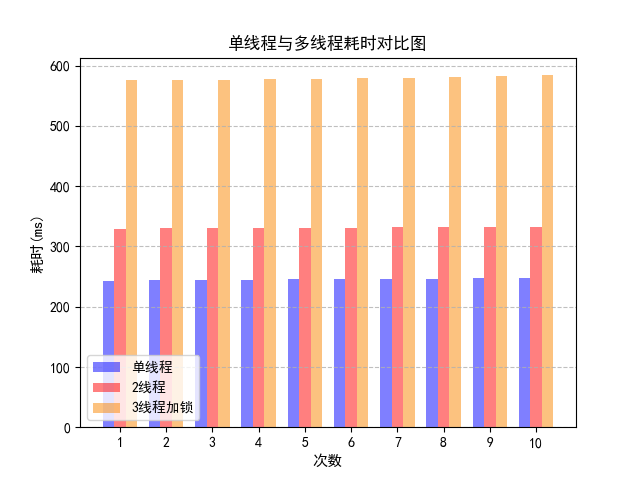
首先观察单线程、2线程和3线程的结果。结果显示，2线程的耗时大于单线程，这是由于线程启停以及线程上下文切换都会引起额外的开销，所以消耗的时间比单线程多。另外主要耗时的线程是apple线程，orrange线程的开销小，所以由于多线程带来的收益没有开销大。从中可以吸取到的经验是，在采用多线程方法设计程序时，如果产生的额外开销大于线程的工作任务，就没有并行的必要。

而3线程的耗时巨大的原因，addx线程和addy线程，由于要竞争同一把锁，所以实际上是串行运行的。比2线程多出的时间则是3线程产生的系统开销。由于访问apple的两个线程访问的是 apple 的不同元素，根本没有加锁的必要，所以可以删除读写锁代码。

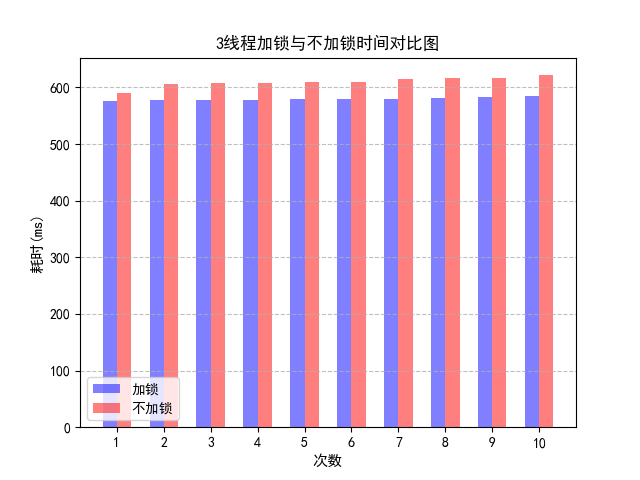
3线程不加锁的效果反而不如3线程加锁，这是由于cache伪共享。伪共享指的是多个线程同时读写同一个缓存行的不同变量时导致的 CPU 缓存失效。在本问题中，尽管 addx 线程中操作的a变量与 addy 线程操作的b变量之间没有任何关系，但由于在主内存中邻近，存在于同一个缓存行之中。如果多个线程的变量共享了同一个 CacheLine，任意一方的修改操作都会使得整个 CacheLine 失效，因为 CacheLine 是 CPU 缓存的最小单位。也就意味着，频繁的多线程操作，CPU 缓存将会彻底失效，降级为 CPU core 和主内存的直接交互。

伪共享问题的解决方法便是字节填充。我们只需要保证不同线程的变量存在于不同的 CacheLine 即可，使用多余的字节来填充可以做点这一点，这样就不会出现伪共享问题。针对这种思路，将apple的数据结构更改如下，并测试不同大小的字节填充带来的结果。

struct apple
{
    unsigned long long a;
    char c[128];  /*32,64,128*/
    unsigned long long b;
};

前文中提到，填充32字节的方案每次运行结果大不相同。这是因为在我的处理器，cache 行的大小为64bytes，可以用如下命令查看cache行大小：

cat /sys/devices/system/cpu/cpu0/cache/index0/coherency_line_size

因此，如果使用32字节做填充，a与b有时会被分配到同一个cache行，从而产生cache伪共享的问题，有时则不会。

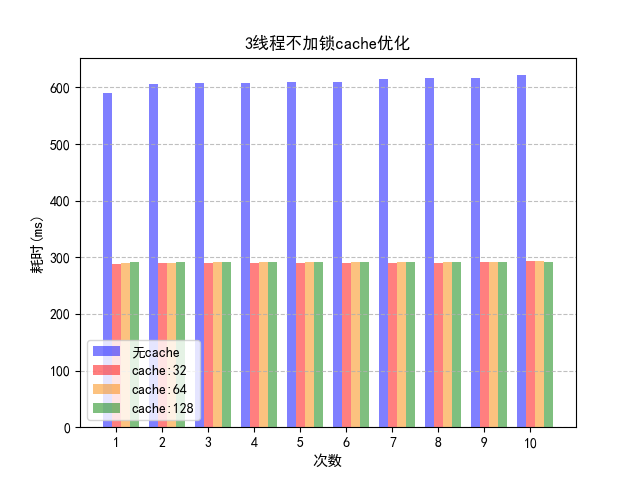
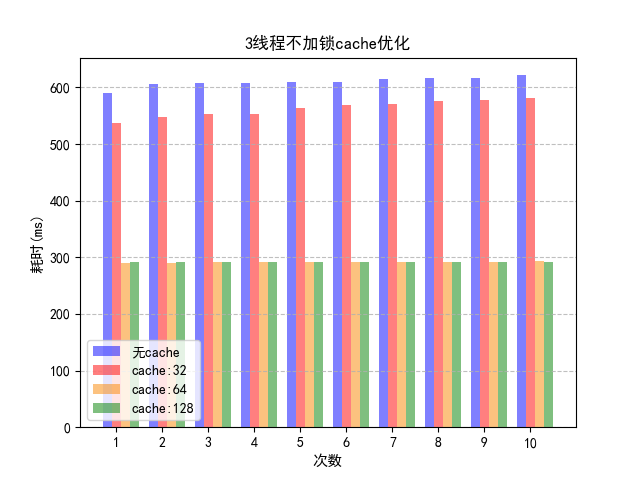
因为使用32字节填充的不稳定性，之后再考虑字节填充时不会采用这种方案。

观察3线程加锁使用cache填充会如何？

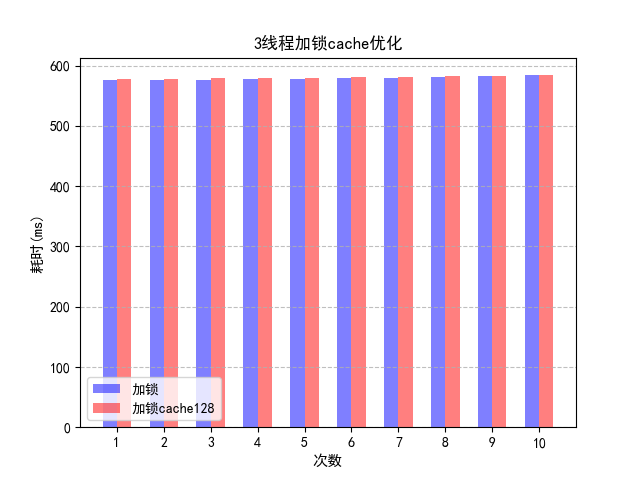
结果是没有什么变化。其原因是加锁的三线程方案效率低下的原因不是 Cache 失效造成的，而是那把锁。

3线程不加锁并行程序带给我们的启示是，在多核和多线程程序设计过程中，要全盘考虑多个线程的访存需求，不要单独考虑一个线程的需求。在选择并行任务分解方法时，要综合考虑访存带宽和竞争问题，将不同处理器和不同线程使用的数据放在不同的 Cache 行中，将只读数据和可写数据分离开。

接下来观察cpu硬亲和力的影响。如果将计算 apple 的线程绑定到一个 CPU 上，将计算 orange 的线程绑定到另外一个 CPU 上，效率是否会有所提高呢？

调整上图的坐标轴，可以得到：

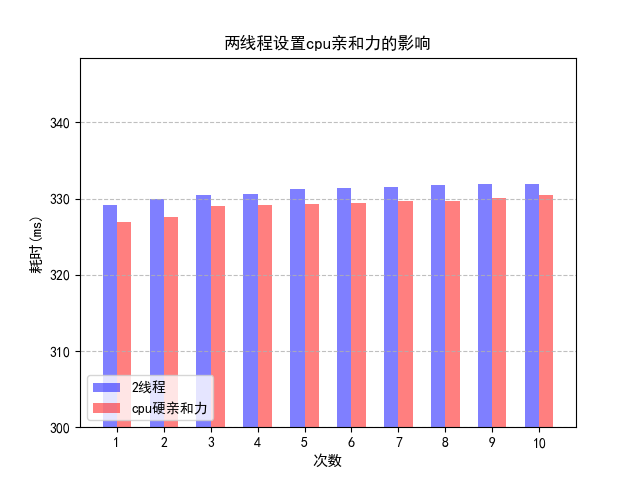
可以看出，设置cpu硬亲和力比不设置的效率略有提升。这是因为在同一个cpu上执行，则cache和LTB中缓存的数据在下一次运行时仍然存在，而进程在cpu之间迁移会提升消耗。Linux 内核进程调度器天生就具有被称为 CPU 软亲和力的特性，这意味着进程通常不会在处理器之间频繁迁移，但是不频繁迁移不代表不迁移。而设置硬亲和力之后，避免这种迁移造成的消耗，在某种程度上硬亲和力比软亲和力具有一定的优势，同时还提高了程序的可靠性。

但是2线程设置cpu硬亲和力的结果仍然不如3线程使用cache优化的结果。这是由于两线程的瓶颈在于大部分时间都消耗在计算 apple 上。如果将apple中addx的部分和addy的部分分别绑定到不同的cpu，效率是否会有提升？

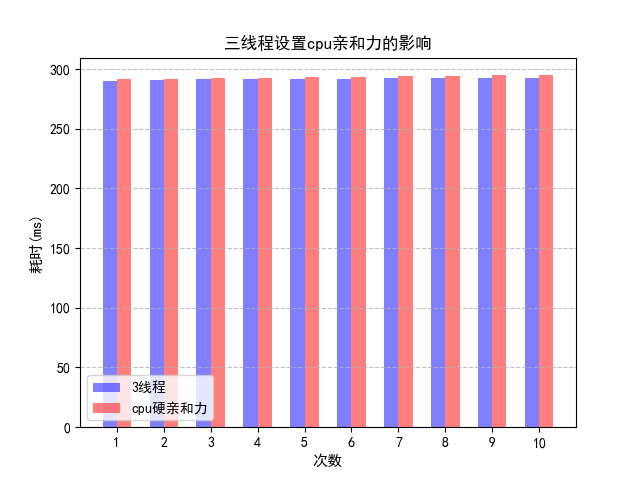
调整上图的坐标轴，可以得到：

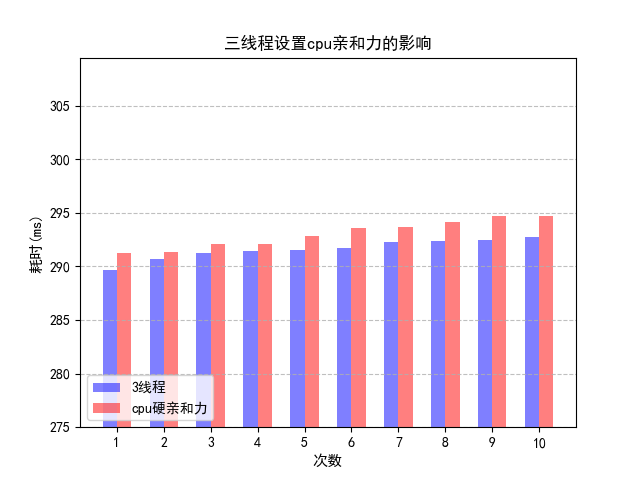
设置亲和力的程序所花费的时间略高于采用 Cache 的三线程方案。由于考虑了 Cache 的影响，排除了一级缓存造成的瓶颈，多出的时间主要消耗在系统调用及内核上，可以通过 time 命令来验证

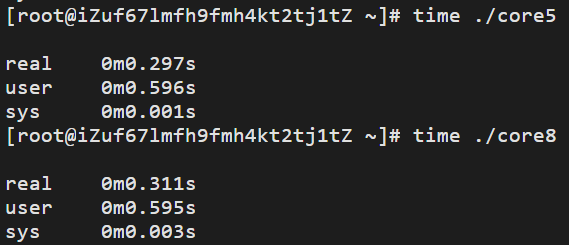
其中./core5是方案五（不设置cpu硬亲和力），./core8是方案八（设置cpu硬亲和力）。这给我们了启示，设置硬亲和力也会提升系统开销。

在实际问题中，我们需要综合考虑复杂均衡、数据竞争、系统开销的问题，以免事倍功半。

根据以上分析及实验，对所有改进方案的测试时间做一个综合对比，如下图所示：

最终的实验结果与实验指导书中的不同之处在于，单线程仍然是最优的方案。推测这是由于多线程造成的系统开销的缘故。其他的结果均与实验指导书一致。

4.6 程序代码

实验代码同附件core.c。

#define _GNU_SOURCE
#include <ctype.h>
#include <malloc.h>
#include <pthread.h>
#include <sched.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <sys/types.h>
#include <unistd.h>
#define gettid() syscall(__NR_gettid)

#define ORANGE_MAX_VALUE 1000000
#define APPLE_MAX_VALUE 100000000
#define MSECOND 1000000

int set_cpu(int i);
long *k_best(int k, int e, int m, void (*fuc)(void));
int cmp(const void *_a, const void *_b);

struct apple4 {
  unsigned long long a;
  char c[128];
  unsigned long long b;
  pthread_rwlock_t rwLock;
};

struct apple3 {
  unsigned long long a;
  char c[64];
  unsigned long long b;
};

struct apple2 {
  unsigned long long a;
  char c[32];
  unsigned long long b;
};

struct apple1 {
  unsigned long long a;
  unsigned long long b;
  pthread_rwlock_t rwLock;
};

struct orange {
  int a[ORANGE_MAX_VALUE];
  int b[ORANGE_MAX_VALUE];
};

int cpu_nums;

inline int set_cpu(int i) {
  cpu_set_t mask;
  CPU_ZERO(&mask);

  if (2 <= cpu_nums) {
    CPU_SET(i, &mask);

    if (-1 == sched_setaffinity(gettid(), sizeof(&mask), &mask)) {
      perror("set cup failed");
      return -1;
    }
  }
  return 0;
}

void *addx__(void *x) {
  //设置cpu硬亲和力
  if (-1 == set_cpu(1)) {
    return NULL;
  }

  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1 *)x)->a += sum;
  }

  return NULL;
}

void *addx__4(void *x) {
  //设置cpu硬亲和力，且考虑cache优化
  if (-1 == set_cpu(1)) {
    return NULL;
  }

  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple4 *)x)->a += sum;
  }

  return NULL;
}

void *addx_(void *x) {
  //加锁
  pthread_rwlock_wrlock(&((struct apple1 *)x)->rwLock);

  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1 *)x)->a += sum;
  }
  pthread_rwlock_unlock(&((struct apple1 *)x)->rwLock);

  return NULL;
}

void *addx(void *x) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1 *)x)->a += sum;
  }

  return NULL;
}

void *addx2(void *x) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple2 *)x)->a += sum;
  }

  return NULL;
}

void *addx3(void *x) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple3 *)x)->a += sum;
  }

  return NULL;
}

void *addx4(void *x) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple4 *)x)->a += sum;
  }

  return NULL;
}

void *addx4_(void *x) {
  int sum;
  pthread_rwlock_wrlock(&((struct apple4 *)x)->rwLock);
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple4 *)x)->a += sum;
  }
  pthread_rwlock_unlock(&((struct apple4 *)x)->rwLock);
  return NULL;
}

void *addy__(void *y) {
  if (-1 == set_cpu(2)) {
    return NULL;
  }

  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1 *)y)->b += sum;
  }

  return NULL;
}

void *addy__4(void *y) {
  if (-1 == set_cpu(2)) {
    return NULL;
  }

  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple4 *)y)->b += sum;
  }

  return NULL;
}

void *addy_(void *y) {
  pthread_rwlock_wrlock(&((struct apple1 *)y)->rwLock);
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1 *)y)->b += sum;
  }
  pthread_rwlock_unlock(&((struct apple1 *)y)->rwLock);

  return NULL;
}

void *addy(void *y) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1 *)y)->b += sum;
  }

  return NULL;
}

void *addy2(void *y) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple2 *)y)->b += sum;
  }

  return NULL;
}

void *addy3(void *y) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple3 *)y)->b += sum;
  }

  return NULL;
}

void *addy4(void *y) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple4 *)y)->b += sum;
  }

  return NULL;
}

void *addy4_(void *y) {
  int sum;
  pthread_rwlock_wrlock(&((struct apple4 *)y)->rwLock);
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple4 *)y)->b += sum;
  }
  pthread_rwlock_unlock(&((struct apple4 *)y)->rwLock);
  return NULL;
}

void* add__(void* x) {
  if (-1 == set_cpu(1)) {
    return NULL;
  }

  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1*)x)->a += sum;
    ((struct apple1*)x)->b += sum;
  }

  return NULL;
}

void* add(void* x) {
  int sum;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    ((struct apple1*)x)->a += sum;
    ((struct apple1*)x)->b += sum;
  }

  return NULL;
}

void func1() {
  // 单线程
  int sum, index;
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  for (sum = 0; sum < APPLE_MAX_VALUE; sum++) {
    test1.a += sum;
    test1.b += sum;
  }

  sum = 0;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }
}

void func2() {
  // 双线程
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, add, &test1);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
}

void func3() {
  //3线程加锁
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_rwlock_init(&test1.rwLock, NULL);
  pthread_create(&ThreadA, NULL, addx_, &test1);
  pthread_create(&ThreadB, NULL, addy_, &test1);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
  pthread_rwlock_destroy(&test1.rwLock);
}

void func4() {
  // 3线程不加锁
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, addx, &test1);
  pthread_create(&ThreadB, NULL, addy, &test1);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
}

void func5_1() {
  // 3线程不加锁cache优化1
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, addx2, &test2);
  pthread_create(&ThreadB, NULL, addy2, &test2);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
}

void func5_2() {
  // 3线程不加锁cache优化2
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, addx3, &test3);
  pthread_create(&ThreadB, NULL, addy3, &test3);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
}

void func5_3() {
  // 3线程不加锁cache优化3
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, addx4, &test4);
  pthread_create(&ThreadB, NULL, addy4, &test4);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
}

void func6() {
  // 3线程加锁cache优化3
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_rwlock_init(&test4.rwLock, NULL);
  pthread_create(&ThreadA, NULL, addx4_, &test4);
  pthread_create(&ThreadB, NULL, addy4_, &test4);

  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
  pthread_rwlock_destroy(&test4.rwLock);
}

void func7() {
  // 2线程设置cpu硬亲和力
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, add__, &test1);

  if (-1 == set_cpu(0)) {
    return;
  }
  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
}

void func8() {
  // 3线程不加锁设置cpu亲和力
  struct orange test;
  struct apple1 test1; 
  struct apple2 test2; 
  struct apple3 test3; 
  struct apple4 test4; 
  pthread_t ThreadA, ThreadB;
  pthread_create(&ThreadA, NULL, addx__4, &test4);
  pthread_create(&ThreadB, NULL, addy__4, &test4);

  if (-1 == set_cpu(0)) {
    return;
  }
  int sum, index;
  for (index = 0; index < ORANGE_MAX_VALUE; index++) {
    sum += test.a[index] + test.b[index];
  }

  pthread_join(ThreadA, NULL);
  pthread_join(ThreadB, NULL);
}

int main(int argc, const char *argv[]) {
  // insert code here...
  long *arr;
  int k = 10;
  int e = 2;
  int m = 200;
  int i;
  long ave, all = 0;
  int funcnum;

  cpu_nums = sysconf(_SC_NPROCESSORS_CONF);

  if(argc <2){
    printf("too few args\n");
    return 1;
  }

  funcnum = atoi(argv[1]);
  switch(funcnum){
    case 1:
      arr = k_best(k, e, m, func1);
      break;
    case 2:
      arr = k_best(k, e, m, func2);
      break;
    case 3:
      arr = k_best(k, e, m, func3);
      break;
    case 4:
      arr = k_best(k, e, m, func4);
      break;
    case 51:
      arr = k_best(k, e, m, func5_1);
      break;
    case 52:
      arr = k_best(k, e, m, func5_2);
      break;
    case 53:
      arr = k_best(k, e, m, func5_3);
      break;
    case 6:
      arr = k_best(k, e, m, func6);
      break;
    case 7:
      arr = k_best(k, e, m, func7);
      break;
    case 8:
      arr = k_best(k, e, m, func8);
      break;
    default:
      printf("wrong arg\n");
      return 1;
  }

  for (i = 0; i < k; i++) {
    printf("%ld\n", arr[i]);
    all += arr[i];
  }
  ave = all / k;
  printf("ave = %ld\n", ave);

  return 0;
}

long *k_best(int k, int e, int m, void (*fuc)(void)) {
  long *arr = (long *)malloc(sizeof(long) * k);
  memset(arr, 0, sizeof(long) * k);
  struct timeval begin, end;
  int i;
  long time_use;
  for (i = 0; i < m; i++) {
    if (gettimeofday(&begin, NULL) < 0) {
      perror("get time failed1");
    }
    fuc();
    if (gettimeofday(&end, NULL) < 0) {
      perror("get time failed2");
    }
    time_use =
        (end.tv_sec - begin.tv_sec) * MSECOND + (end.tv_usec - begin.tv_usec);
    printf("%d: %ld us\n", i, time_use);
    if (i < k) {
      arr[i] = time_use;
      if (i == k - 1) {
        qsort(arr, k, sizeof(long), cmp);
        if (arr[k - 1] <= arr[0] * (1.0 + (float)e / 100)) {
          printf("break when i = %d\n", i);
          return arr;
        }
      }
    } else {
      if (time_use < arr[k - 1]) {
        arr[k - 1] = time_use;
        qsort(arr, k, sizeof(long), cmp);
      }
      if (arr[k - 1] <= arr[0] * (1.0 + (float)e / 100)) {
        printf("break when i = %d\n", i);
        return arr;
      }
    }
  }
  printf("Done!\n");
  return arr;
}

int cmp(const void *_a, const void *_b) {
  long *a = (long *)_a;
  long *b = (long *)_b;
  return *a - *b;
}

Sinkers

【北邮大三上操作系统】第五组多核多线程编程及性能分析

第五组多核多线程编程及性能分析

1 实验要求

2 实验环境

3 实验内容1 观察实验平台物理 cpu、CPU 核和逻辑 cpu 的数目

3.1 实验目的

3.2 实验方法

3.3 运行结果及分析

4 实验内容2 单线程/进程串行 vs 2 线程并行 vs 3 线程加锁并行程序

4.1 实验目的

4.2 实验内容

4.3 实验设计原理

4.4 实验步骤

步骤一单线程/样例程序

步骤二 2线程

步骤三 3线程加锁

步骤四 3线程不加锁

步骤五 cache优化3线程不加锁

步骤六 cache优化3线程加锁

步骤七 2线程设置cpu硬亲和力

步骤八 3线程设置cpu硬亲和力

步骤九使用k-best方法计算每种方案的执行时间并统计

4.5 实验结果及分析

方案一单线程/样例程序运行结果

方案二 2线程运行结果

方案三 3线程加锁运行结果

方案四 3线程不加锁运行结果

方案五 cache优化3线程不加锁运行结果

方案六 cache优化3线程加锁运行结果

方案七 2线程设置cpu硬亲和力运行结果

方案八 3线程设置cpu硬亲和力运行结果

实验结果统计与分析

4.6 程序代码

【北邮大三上操作系统】第四组线程的同步与互斥

【北邮大三下操作系统】第三组进程通信——管道通信与信号通信

Comments NOTHING

取消回复

Sinkers

第五组 多核多线程编程及性能分析

1 实验要求

2 实验环境

3 实验内容1 观察实验平台物理 cpu、CPU 核和逻辑 cpu 的数目

3.1 实验目的

3.2 实验方法

3.3 运行结果及分析

4 实验内容2 单线程/进程串行 vs 2 线程并行 vs 3 线程加锁并行程序

4.1 实验目的

4.2 实验内容

4.3 实验设计原理

4.4 实验步骤

步骤一 单线程/样例程序

步骤二 2线程

步骤三 3线程加锁

步骤四 3线程不加锁

步骤五 cache优化3线程不加锁

步骤六 cache优化3线程加锁

步骤七 2线程设置cpu硬亲和力

步骤八 3线程设置cpu硬亲和力

步骤九 使用k-best方法计算每种方案的执行时间并统计

4.5 实验结果及分析

方案一 单线程/样例程序运行结果

方案二 2线程运行结果

方案三 3线程加锁运行结果

方案四 3线程不加锁运行结果

方案五 cache优化3线程不加锁运行结果

方案六 cache优化3线程加锁运行结果

方案七 2线程设置cpu硬亲和力运行结果

方案八 3线程设置cpu硬亲和力运行结果

实验结果统计与分析

4.6 程序代码

【北邮大三上操作系统】第四组 线程的同步与互斥

【北邮大三下操作系统】第三组 进程通信——管道通信与信号通信

Comments NOTHING

取消回复

第五组多核多线程编程及性能分析

步骤一单线程/样例程序

步骤九使用k-best方法计算每种方案的执行时间并统计

方案一单线程/样例程序运行结果

【北邮大三上操作系统】第四组线程的同步与互斥

【北邮大三下操作系统】第三组进程通信——管道通信与信号通信